INTRODUCTION
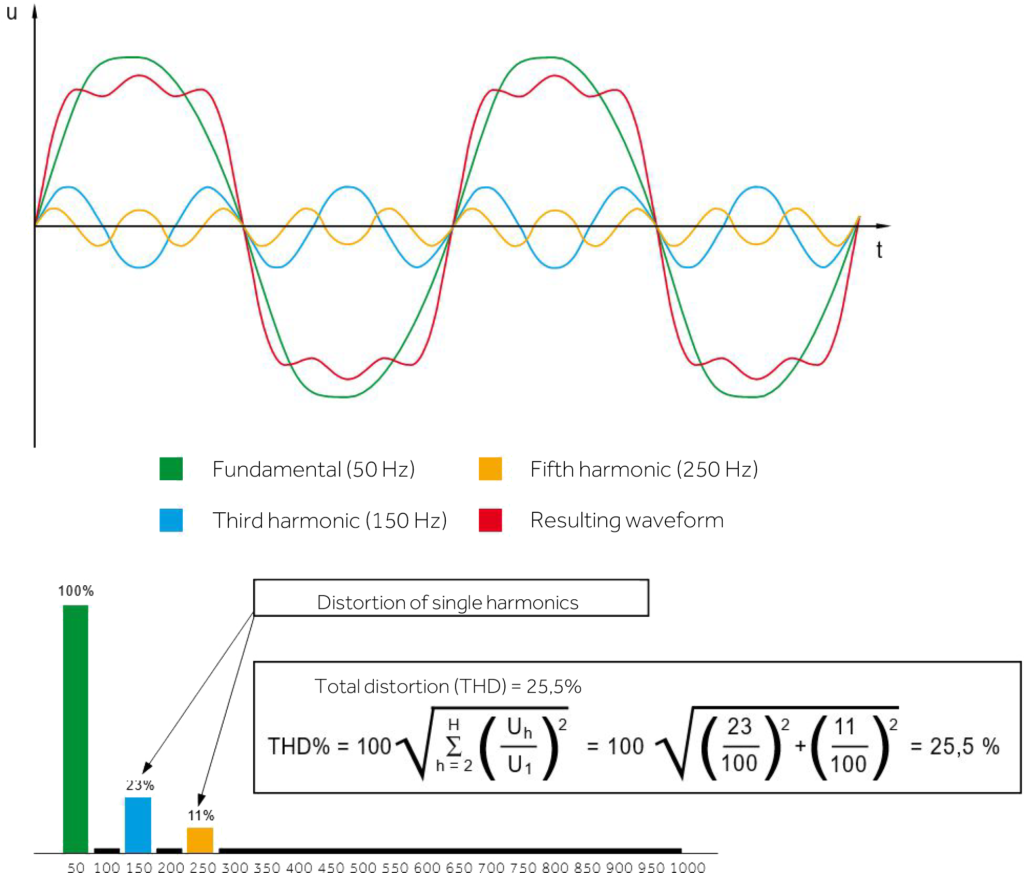
Given a sinusoidal magnitude (fundamental) a sinusoidal magnitude of multiple frequency is defined as harmonic. The order of the harmonic is the ratio between its frequency and that of the fundamental: for example, if the fundamental is at 50Hz the harmonic of the third order, orthird harmonic, has a frequency of 150Hz.
The sum of the fundamental and of the harmonics gives rise to a resultant periodic, but not sinusoidal, function (distorted waveform). A distorted waveform is therefore equivalent to the presence of harmonics and vice versa. Generalizing, any periodic function can be broken down into a series of sinusoidal functions (Fourier series). The electric generators supply a
sinusoidal voltage at 50Hz, butthe currentflowing in the load is not always sinusoidal.
The current is not sinusoidal when the load has a variable impedance during the T period (equal to 20ms at 50Hz); in other words, when the load voltage / current characteristic is not linear. In these cases it is said, in short, that the load is not linear.
Other typical examples of non-linear loads are rectifiers (battery chargers, welders, electrolytic cells, etc.), inverters, electronic starters, variable frequency motor drives, electronic switching power supplies, discharge lamps (fluorescent tubes, sodium lamps, mercury vapor lamps, etc.). A non-sinusoidal current causes distorted voltage drops in the circuit, so that even the voltage at one point in the circuit becomes distorted. The voltage along the line is given by the voltage supplied by the transformer, minus the distorted voltage drop. The voltage distortion therefore increases with the voltage drop, that is with the distance from the transformer and with the impedance ofthe line.
In summary, the distortion in a point of the electric network is the smaller the greater the current (power) of short circuit in that point. The electrical network may be that of the utility company, disturbed by users who produce harmonics, or the internal one of the user himself.
A distorted voltage causes harmonics even on linear loads. The presence of harmonics affects all phenomena related to frequency increase. For example, the capacitive reactance decreases and therefore the current in the capacitors increases, which can be damaged or even resonate; the losses in the iron increase due to hysteresis and parasitic currents; increase cable losses, etc.
Itis easy to imagine that harmonics can cause electronic equipment to malfunction.
POWER FACTORCORRECTION OF MV / LV TRANSFORMERS
The problem of harmonics is part of the wider problem of electromagnetic compatibility. The so-called good education is a set of rules that aim to make more people who live in the same field compatible with each other, making sure that one does not disturb the others beyond certain limits and vice versa; at the same time each person must have a minimum oftolerance towards others.
Electromagnetic compatibility is the equivalent of good education in the electrical sector: the rules for electromagnetic compatibility establish the limits of emission of disturbances and the level of immunity to disturbances themselves, so that more electrical appliances arranged in the same space and / or powered from the same network can work properly.
The disturbances can be irradiated by means of the electromagnetic field, or be
transmitted (conducted) through the network. Harmonics are a typical example of conducted disturbance.
The regulations establish, for all those devices that produce harmonics, a limit to the harmonic content and, for devices sensitive to harmonics, the level of immunity to the harmonics themselves
The total distortion factor was introduced to evaluate the effect of all the harmonics (THD):
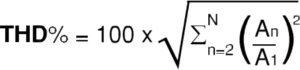
where:
An is the amplitude of the harmonic of order n
A1 is the amplitude of the fundamental
N is the highest harmonic order considered
In the case of a single harmonic the distortion factor is reduced to the percentage value (in amplitude) of the harmonic with respect to the fundamental. The distortion factor is often indicated with THDf to highlight that it is calculated with respect to the value of the fundamental. In some cases the THDr is also specified, ie the distortion factor calculated with respectto the true effective value ofthe measured quantity.
FEATURES OF ELECTRIC SYSTEMS
The effects of one or more harmonic sources on an electrical power system depend mainly on the characteristic frequency response. Non-linear devices or loads can be represented as sources of harmonic currents so the harmonic distortion of voltage in the system depends on the impedance-frequency characteristic.
The frequency response ofthe system can be influenced by several factors.
System short-circuit powers
The short-circuit power of the system is an indication of the impedance of the system at the fundamental frequency in a predefined point of the system. For simple power supply systems this is also a measure of the impedance of the system at harmonic frequencies if it is multiplied by the order of harmonic. The systems with the highest short-circuit power ratings are characterized by limited values of the system / system impedance and therefore by limited voltage distortions,with the same harmonic current source.
Capacitors and power cables
The capacitors used to improve the power factor of the systems and the insulated power cables are the components that most influence the frequency response of a system. The connection of capacitors can cause resonance conditions (series or parallel) that can amplify the level of the harmonics. The line capacities of the distribution cables and in general of the insulated cables can be considered in parallel with the inductance of the system so they are similar to shunt capacitors. Normally the groups of PFC capacitors are
dominant in the industrial distribution systems and their effect prevails over that caused by the capacities ofthe cables
Load Features
The load has two important effects on the frequency response characteristic:
• the resistive part reduces the amplitude of the harmonic level near the parallel
resonance frequency;
• motors and other dynamic loads, which contribute to the short-circuit power of the system, can modify the frequencies to which resonance phenomena may occur: these loads appear in parallel with the short-circuit inductance of the system when resonance frequencies are calculated.
CONDITIONS OF RESONANCE
The resonance conditions are to be considered the most important factors that influence the level of harmonics in the systems.
Considering the circulation of current harmonics, the parallel resonance condition is equivalent to a high impedance while the series resonance is equivalent to a low impedance. When these currents see a high impedance due to parallel resonance conditions there are significant voltage distortions while in the case of resonance, current amplifications are shown. Therefore it is very important to be able to evaluate, in a more or less detailed way, the frequency response of the system to avoid resonance problems in the systems.
CIRCULATION OFHARMONIC CURRENT
Current harmonics tend to flow from non-linear loads (harmonic sources) through lower impedance paths, normally the power sources. The impedance of the power supplies is normally much lower than those of the parallel paths represented by the loads. However, the harmonic currents will restart according to the impedance ratio. Higher order harmonics, on the other hand, will prefer compound loads or capacitors because at high frequencies they have a low impedance.
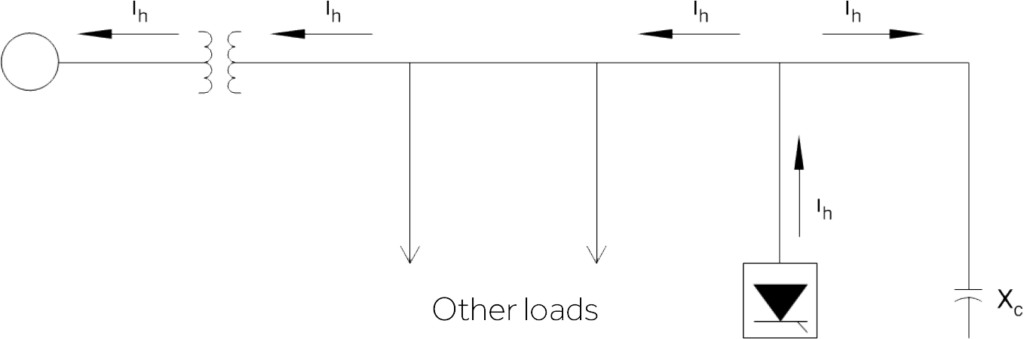
Parallel resonance
Parallel resonance occurs when the inductive and capacitive reactance, seen from the connection point
of a load, are, at a specific frequency, equal. If the combination of power factor correction capacitors and line or transformer inductances are in
parallel resonance near one of the harmonics generated by a non-linear load, a high distortion of the voltage on the capacitors will occur; in fact, due to the high value of the impedance equivalent to the
resonance frequency, even a small harmonic current can cause high voltage distortions.
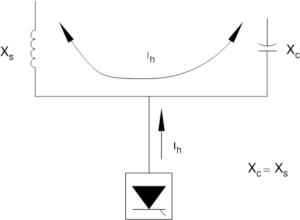
Series resonance
Parallel resonance occurs when the inductive and capacitive reactance, seen from the connection point of a load, are, at a specific frequency, equal.
If the combination of power factor correction capacitors and line or transformer inductances are in parallel resonance near one of the harmonics generated by a non-linear load, a high distortion of the voltage on the capacitors will occur; in fact, due to the high value of the impedance equivalent to the resonance frequency, even a small harmonic current can cause high voltage distortions.
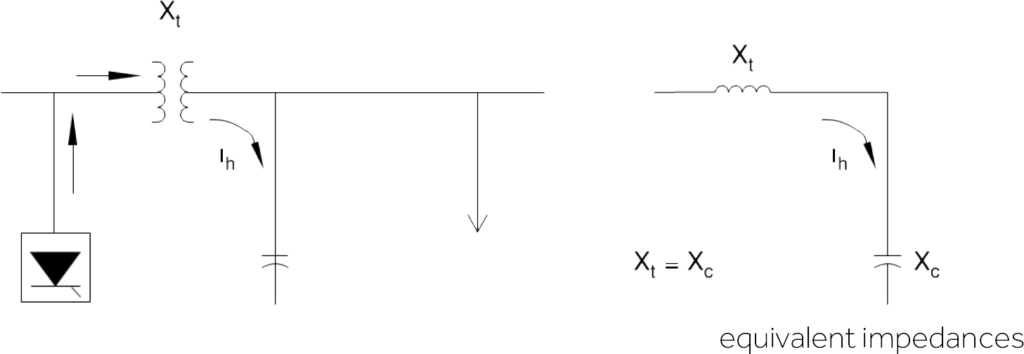
Analysis method
To calculate the resulting harmonic level in a system due to harmonic sources, it is necessary to know the characteristics of the harmonic sources and the frequency response of the system. Many sources of harmonics can be represented as ideal current sources: the hypothesis on which this assumption is based is that the voltage of the system is not distorted. Once the characteristic of the harmonic source has been determined, the system response can be calculated; Important elements of the model used to perform these calculations are:
• equivalent system short circuit impedance,
• capacitors,
• characteristics ofthe lines and cables ofthe system,
• characteristics ofthe loads.
The analysis of the system to be performed through relatively simple calculations for some industrial plants. However, to determine significant results, many systems require simulation programs that allow the system’s response to different frequencies to be represented.
Simplified calculation
By simplifying the industrial plants with the scheme shown below it is possible to determine the resonance frequency very easily with the following formula:

where:
hr is the resonance frequency, as a multiple of the fundamental frequency
MVASC is the short-circuit power at the point where the PFC capacitors are inserted, expressed in MVA
MVAcap is the installed capacitive reactive power, expressed in Mvar

To be able to complete this verification, as a first approximation, it can be considered as the short-circuit power the only short-circuit power of the MV / LV transformer that supplies the system / system in question, so that:
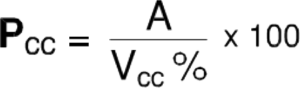
where:
A is the power of the MV / LV transformer, expressed in kVA
Vcc is the percentage short-circuit voltage of the MV / LV transformer
In cases where the capacitors are stepped through an electronic regulator, the calculation must be repeated, if necessary, for all the possible combinations of the individual steps because for each reactive power value inserted in the network there will be as many frequency values towhich parallel resonance conditions may correspond.
POWER FACTORCORRECTIONINTHE PRESENCE OFHARMONICS
Power factor correction of non-linear electrical loads is often hampered by the current harmonics produced or injected on the power line. An example of a typical system / system is shown in figure 6: in the left part of the figure a three-phase alternate network is shown, represented with its own line inductance L1 and with the electromotive vacuum force E; it supplies a three-phase rectifier bridge which, in turn, is connected to a direct currentload; the possible PFC capacitors Cr.
The effects on the line of the fundamental component and of the harmonic components of the current absorbed by the converter can be studied with the equivalent schemes drawn on the right side: they are the equivalent circuits side alternated to the frequency of 50Hz and to a generic harmonic frequency of value k * 50Hz , treating the static converter as a current generator.
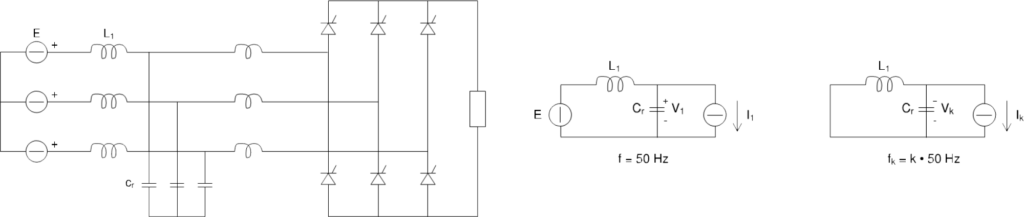
Supposing the amplitude of the generic harmonic current, the relative voltage harmonic at the input terminals ofthe converter can be evaluated with the following formula

where:
Zk is the network impedance module seen by the converter at the k * 50Hz frequency
In the presence of power factor correction capacitors, the impedance in question is that of the parallel between the line inductance and the capacitance ofthe capacitors themselves; its module can take the trend outlined in figure 7.
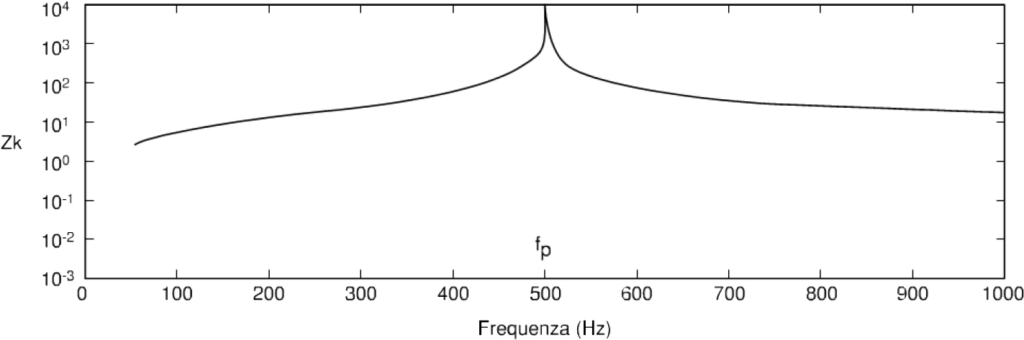
It highlights a phenomenon of resonance parallel to the frequency given by:
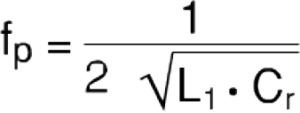
The frequency fp therefore depends on the characteristics of the line and on the power factor correction capacitors. The fp values are obviously greater than 50Hz, but in any case they often fall within the field in which the most significant harmonic frequencies of the converters fall.
It is also understood that the harmonics of frequency current close to that of parallel resonance cause large harmonic voltages and, consequently, intense and often intolerable harmonic currents in the power factor correction capacitors and in the supply line. Ultimately there is an amplification of the harmonics of frequency current close to that of parallel resonance, with the manifestation of consistent deformations of the voltage.
To avoid these drawbacks, in non-high power applications, inductances Lr are arranged in series with the appropriate power factor correction capacitors so as to compose, with the capacitors Cr, a series LC branch as shown in the box of figure 8.
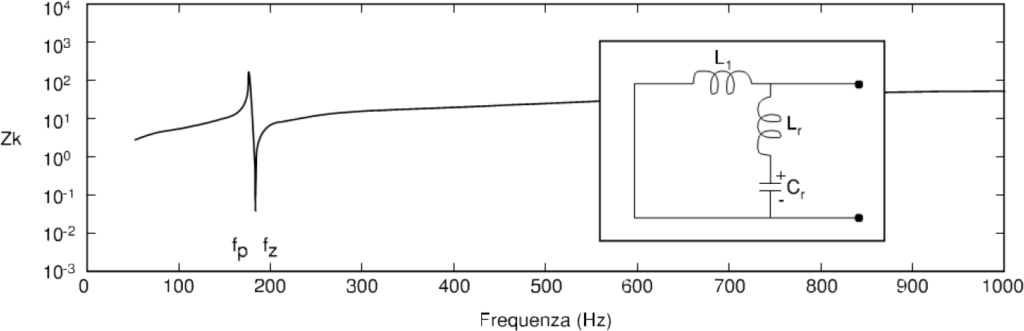
The inductance Lr is chosen so as to have the resonance frequency of the LC series at a value lower than that of the lower harmonic frequency, usually set around 200Hz, and in any case is given by the relation:
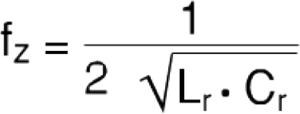
Recalling that in a reactive bipole the series resonance frequencies and parallel frequencies (resonance and anti-resonance) alternate each other, the resulting trend of the equivalent impedance module seen by the converter will ultimately be the type of figure 8; it can be shown thatthe frequency is:
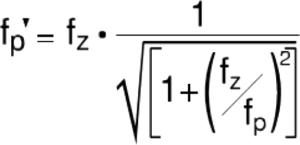
The dimensioning of Lr is carried out based on the previous relation after having set Cr, according to the needs of power factor correction and having chosen a value fz for which fp’ is sufficiently distantfrom the harmonic frequencies, so as notto trigger exaltations of no harmonic component of voltage and current. Observe that while fz depends only on the parameters of the power factor correction system, fp also depends, through fp, on the parameters ofthe network that are usually more uncertain and variable.
FILTERING OFHARMONIC CURRENTS
The presence of non-sinusoidal currents in industrial plants produces undesirable phenomena and in some situations real operating anomalies, which are greater the greaterthe intensity ofthe harmonic components.
In the case of industrial plants where the power of the loads can be even some hundreds of kVA and any harmonic current components of the order of several tens or hundreds of amperes, the operating conditions may not be acceptable: for example an automatic power factor correction board must be dimensioned, it may not be sufficient to create a panel capable of avoiding the exaltation of the harmonic components, but a real action of eliminating harmonics must also be performed.
FILTERING OFHARMONIC CURRENTS
Passive filters are the traditional means of solving problems of containing disturbances caused by non-linear loads and are connected in parallel to the load to be filtered. The equipment consists of several LC branches in each of which each group of capacitors is connected in series with an inductance dimensioned to have the corresponding resonance frequency coinciding with one of the harmonic frequencies of interest. The system thus composed constitutes a preferential path through which the harmonic currents find a way of reclosing and do not affectthe upstream network.
As mentioned, the insertion of passive filters in the network modifies the impedance of the network at different frequencies and alters the frequency response of the electrical system. Therefore it is an operation to be performed with caution because it could generate phenomena of resonance, that is an exaltation of the disturbances and of the negative effects connected to them,ratherthan their attenuation.
Another particular aspect linked to passive filtering is that the filter represents a short circuit for the harmonic to which it is tuned (if the resistances of the filter are neglected) and in the choice of the most suitable device the possibility must be assessed that it can absorb currents harmonics also generated by other polluting loads present in the network.
On the other hand, due to their simplicity of implementation and cost-effectiveness, passive filters are currently the most widely used elements for the reduction of disturbances in distribution networks. Ultimately the practical use of passive filters cannot disregard a series of plant problems that must be known to correctly determine the performances.
a) The characteristics of the filtering depend on the impedance of the network. Even if the filter is perfectly tuned to the frequency you want to eliminate, it will always present some resistance. The harmonic current will flow partly towards the network in greater quantities the lower the impedance of the network with respect to that of the filter. In other words, the filtering effectis lowerthe greaterthe short circuit power ofthe network.
b) The operation of the filters is affected by the presence of any further distorting users connected to other nodes in the networkwhich could cause overload conditions.
c) Passive filters are not suitable for loads with rapidly changing currents. Unless you make electronic insertion systems capable of adjusting the number of elements inserted, the delay between a sudden load increase and the insertion of the new step and of the order of a few tens of seconds and therefore are not suitable for loads where the current varies continuously and rapidly overtime.
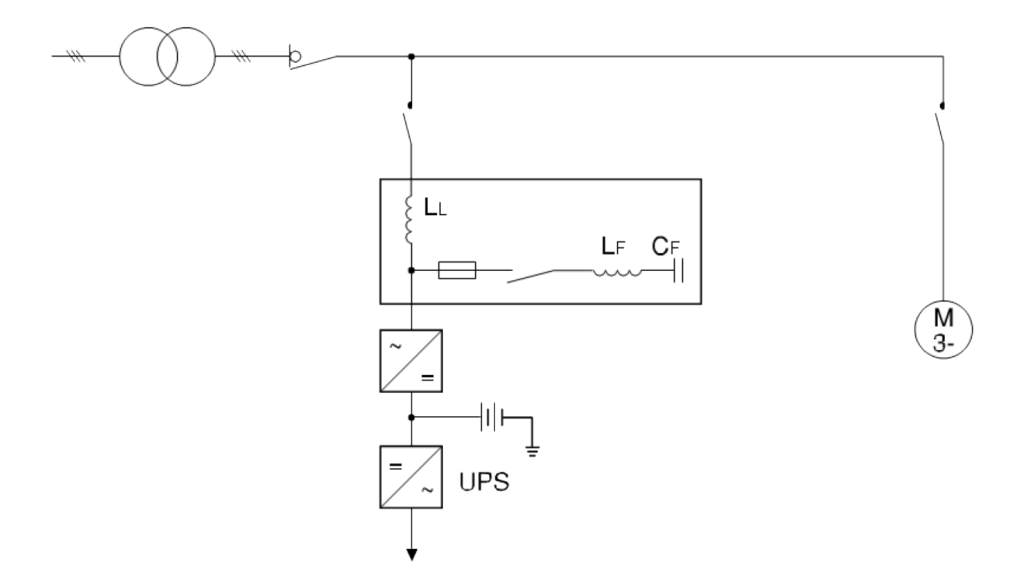
As can be seen from the type of connection of the filter with respect to the load, the line inductance is covered by the load current; consequently this arrangement and type of filters are adopted with loads characterized by a practically constant operating regime, a typical example is the UPS, and with power up to a few hundred kVA.
In the case of large power loads or with time varying current absorption, several sections or filter branches can be used, suitably connected in parallel and controlled by an amperometric signal. In this way it is possible to obtain a modular system able to adapt to the load variation and to the limit able to be easily adapted to new situations or plant configurations with harmonic distortions greater than those initially envisaged due to the installation of new
equipment.
In order to uniformly distribute the harmonic current between one filter step and another and to avoid overloads due to the inevitable differences between the capacitance and inductance values of the LC groups, a second contactor can be used that connects the groups in parallel as see in figure 10.
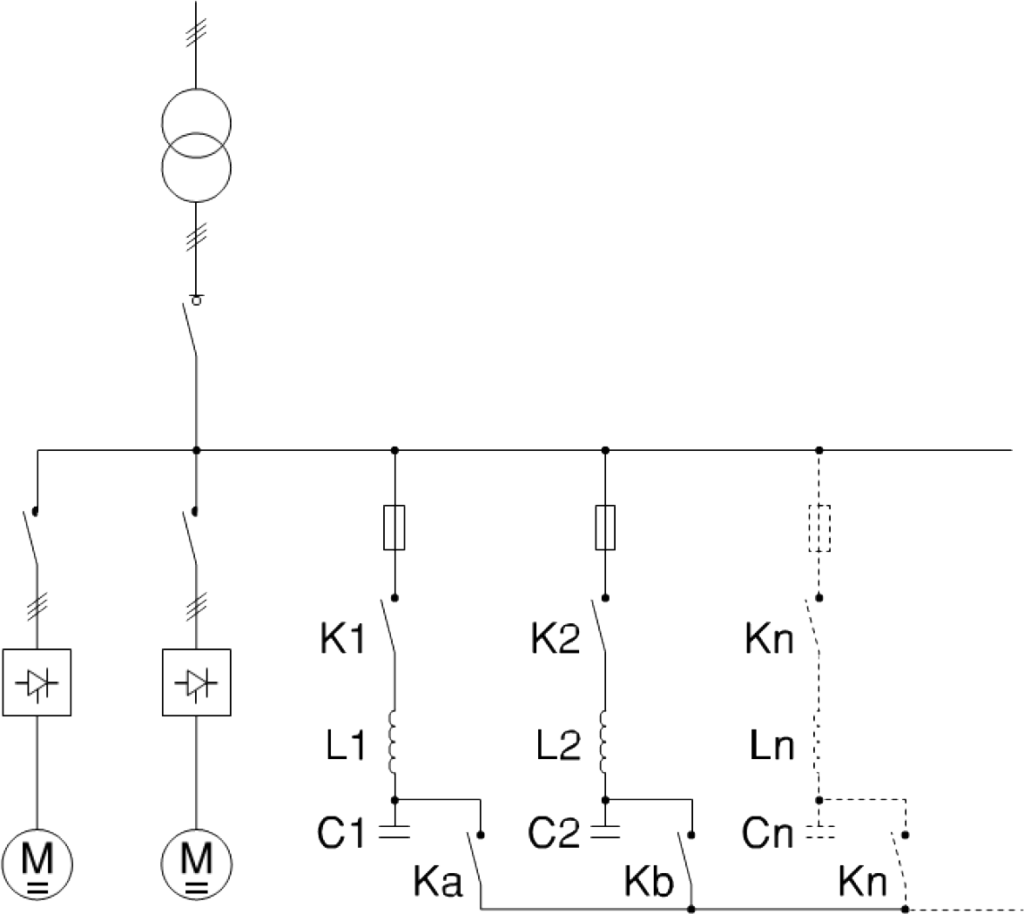
With this arrangement, the different LC steps / branches have all the inductances and all the capacitors connected in parallel and therefore the constructive differences of the different components can be compensated.